2数と16進数の変換方法
2進数から16進数、16進数から2進数への変換方法について説明します。
2進数から16進数への変換
2進数は、0と1しか数字がありません。このため、1 + 1は10となり繰り上がりします。
16進数は、0からFまでの数字があります。このため、F + 1で10となり繰り上がりします。
以下は、2進数の3つの数字を取り上げ、16進数に変換した時の対応表です。
| 2進数 | 1111 | 1111 1111 | 1111 1111 1111 |
|---|---|---|---|
| 16進数 | F | FF | FFF |
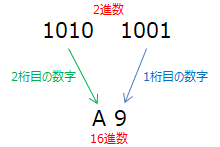
2進数の4桁(1111)までが16進数の1桁(F)、8桁(1111 1111)までが16進数の2桁(FF)、12桁(1111 1111 1111)までが16進数の3桁(FFF)になる事が分かります。つまり、2進数の4桁が16進数の1桁に該当する事になります。
2進数の1〜4桁で数字が変わっても、16進数に影響があるのは1桁目だけです。例えば、2進数の10 0000は16進数で20になりますが、10 0001は16進数で21になり、1桁目だけが変わります。又、5桁目〜8桁目で数字が変わると、16進数の2桁目が変わります。
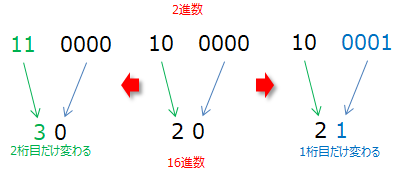
このように、2進数の各4桁が16進数の1桁の数字に影響するため、16進数への変換では2進数を4桁毎に区切って計算すれば良い事が分かります。
又、4桁の2進数から16進数への変換ですが、一旦10進数に変換します。2進数の各桁は、10進数では以下の数字が対応します。
| 2進数 | 1 | 10 | 100 | 1000 |
|---|---|---|---|---|
| 10進数 | 1 | 2 | 4 | 8 |
この10進数の1、2、4、8だけを使って計算します。例えば、2進数1010であれば1000と10の組み合わせのため、対応する10進数を使って8 + 2 = 10となります。これは、16進数でAとなります。
上の対応表がなくても、2進数で1桁上がると対応する10進数が2倍になると覚えて下さい。そうすれば、1、2、4、8の数字が出てくると思います。(詳細は、「2進数と10進数の変換」をご参照下さい)
これを基本として、2進数の10 1100 1010 0100を16進数に変換してみます。
| 元の数字(2進数) | 10 | 1100 | 1010 | 0100 |
|---|---|---|---|---|
| 10進数 | 2 | 8 + 4 = 12 | 8 + 2 = 10 | 4 |
| 16進数 | 2 | C | A | 4 |
結果は、2CA4です。
2進数から16進数変換の練習問題
以下は、変換の練習問題です。2進数の「元の数字」を16進数に変換します。「答え」ボタンをクリックすると答えが表示されます。又、「クリア」ボタンをクリックすると違う問題が出ます。
16進数から2進数への変換
16進数の1桁が2進数の4桁に対応するため、16進数から2進数へ変換するには1桁毎に2進数へ変換すれば良い事になります。
1桁の16進数をまず10進数で表現します。16進数では、10進数の0〜15が1桁で表せます。これを、先ほどの1、2、4、8だけ使って足し算して表します。
例えば、16進数のCであれば10進数で12なので、8 + 4です。1、2、4、8は2進数では以下が対応します(先ほどの対応表とは逆です)。
| 10進数 | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| 2進数 | 1 | 10 | 100 | 1000 |
8が1000、4が10に対応するため、1000 + 10 = 1010になります。2進数の足し算は、10進数と同じです。又、既に説明したように、10進数で2倍になると対応する2進数が1桁上がると覚えておけば、上の表がなくても計算出来ます。
これを基本として、16進数のC1A8を2進数に変換してみます。
| 元の数字(16進数) | C | 1 | A | 8 |
|---|---|---|---|---|
| 10進数 | 12 = 8 + 4 | 1 | 10 = 8 + 2 | 8 |
| 2進数(式) | 1000 + 100 | 0001 | 1000 + 10 | 1000 |
| 2進数(結果) | 1100 | 0001 | 1010 | 1000 |
結果は、1100 0001 1010 1000です。
16進数から2進数変換の練習問題
以下は、変換の練習問題です。2進数の「元の数字」を10進数に変換します。「答え」ボタンをクリックすると答えが表示されます。又、「クリア」ボタンをクリックすると違う問題が出ます。