2進数と10進数の変換方法
2進数から10進数、10進数から2進数への変換方法について説明します。
2進数から10進数への変換
2進数は、0と1しか数字がありません。このため、1 + 1 = 10となり繰り上がります。以下は、2進数の0〜100までを10進数に変換した時の対応表です。
| 2進数 | 0 | 1 | 10 | 11 | 100 |
|---|---|---|---|---|---|
| 10進数 | 0 | 1 | 2 | 3 | 4 |
上記対応表は、例えば2進数の100は、10進数では4になることを示しています。
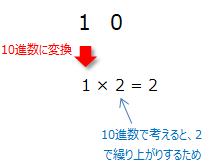
対応表を使わない場合、2進数の10を10進数に変換するのは1 × 2 = 2で計算出来ます。10の2桁目は1です。これに2を掛けているのは、10進数で考えると2で繰り上がるためです。
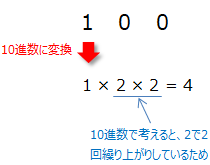
2進数の100は、上の対応表から10進数では4になる事が分かります。これも、1 × 2 × 2 = 4で計算出来ます。2を2回掛けているのは、3桁目は2回繰り上がっているためです。
これは、1 × 22とべき乗で表記出来ます。赤字が底で、青字の小さい数字はべき指数と呼ばれます。べき指数は、2を何回掛けるかを示します。
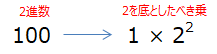
10進数では、10 = 1 × 10、100 = 1 ×10 × 10と桁が増える度に10倍になります。2進数も10進数に変換した場合、10 = 1 × 2、100 = 1 × 2 × 2と桁が増える度に2倍になります。このため、2進数から10進数に変換するためには、桁が増える度にべき指数を1増やせば良い(2倍にすれば良い)事になります。
これを基本として、1010を10進数に変換してみます。
| 桁 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|
| 元の数字(2進数) | 1 | 0 | 1 | 0 |
| 2を底としたべき乗 | 1 × 23 | 0 | 1 × 21 | 0 |
| 10進数 | 1 × 2 × 2 × 2 = 8 | 0 | 1 × 2 = 2 | 0 |
上記から、2進数の1010は10進数に変換すると、8 + 2 = 10となります。
数字が大きくなっても、桁数-1をべき指数にして計算すれば良いだけです。このため、式は簡単に作れます。もう1つの例として、2進数10100を10進数に変換します。
最初の1は5桁目なので、べき指数を4にします。次の1は3桁目なので、べき指数を2にします。式は24 + 22となり、結果は20です。
べき乗で計算するのは面倒ですが、慣れてくると暗算も可能です。最上位桁の1は5桁目なので2、4、8、16と2倍しながら4回数えます。次の1は3桁目なので、2、4と2倍しながら2回数えます。
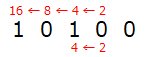
それぞれ最後に数えた16と4を足して、20と結果が出ます。
2進数から10進数変換の練習問題
以下は、変換の練習問題です。2進数の「元の数字」を10進数に変換します。「答え」ボタンをクリックすると答えが表示されます。又、「クリア」ボタンをクリックすると違う問題が出ます。
10進数から2進数への変換
2進数は、桁が増える度に2倍になると説明しました。つまり、10進数で言えば2→4→8→16→32の時に桁が増える事になります。
| 10進数 | 2 | 4 | 8 | 16 | 32 |
|---|---|---|---|---|---|
| 2進数 | 10 | 100 | 1000 | 10000 | 100000 |
10進数の10を2進数に変換してみます。10進数の10は、上の表にある8と16の間の数字です。このため、10を超えない数字の8を使って、10 = 8 + 2に分解します。
表で、10進数の8は2進数で1000が該当します。2は、10が該当します。つまり、10進数の10を2進数に変換すると、1000 + 10 = 1010となります。

対応表がない場合でも、2を何回掛けるとその数字を超えない最大値かを考えると、分解する数字が分かります。10であれば、2 × 2 × 2 = 8です。これで10は、8と残りの数字(例では2)に分解出来る事が分かります。又、掛けた回数がべき指数(例では23)のため、2進数に変換した時の0の数(例では1000のように0が3つ)になります。
これを基本として、10進数の100を2進数に変換してみます。
- ・100の分解
- 100は、26 = 64が超えない最大値です。27 = 128では100を超えてしまいます。このため、100 = 64 + 36に分解出来ます。64は、2進数に変換すると0が6個付きます。
- ・36の分解
- 36は、25 = 32が超えない最大値です。このため、36 = 32 + 4に分解出来ます。32は、2進数に変換すると0が5個付きます。
- ・4の分解
- 4は、22です。分解する必要がなく、2進数に変換すると0が2個付きます。
まとめると、以下になります。
| 元の数字(10進数) | 100 | ||
|---|---|---|---|
| 分解した数字 | 64 | 32 | 4 |
| 2を底としたべき乗 | 1 × 26 | 1 × 25 | 1 × 22 |
| 2進数 | 1000000 | 100000 | 100 |
つまり、10進数の100は64 + 32 + 4に分解出来ます。それぞれ2進数に変換すると、1000000 + 100000 + 100 = 1100100になります。
10進数を分解する時に利用できる数字が、2、4、8、16、32、64・・・と2倍ずつの数字と理解できれば、計算も楽になります。
10進数から2進数変換の練習問題
以下は、変換の練習問題です。2進数の「元の数字」を10進数に変換します。「答え」ボタンをクリックすると答えが表示されます。又、「クリア」ボタンをクリックすると違う問題が出ます。